The coefficient of performance refers to the change in ratio in the heat released at an output compared to the work that must be performed in order to release that heat. This measurement is typically used to measure the output of heat pumps, however, it can be used for other measurements as well. The coefficient of performance is sometimes abbreviated COP or CP. Various equations are used to determine the COP in different applications.
When deriving or determining the coefficient of performance, the first rule of thermodynamics is important to remember. This rule states that energy can be changed, but it cannot be destroyed nor can it be created. As a result of this rule, the equations used to determine the coefficient of performance generally begin by considering the heat that is taken in from the air by the reservoir for cold heat and the heat that is released from the reservoir for hot air.
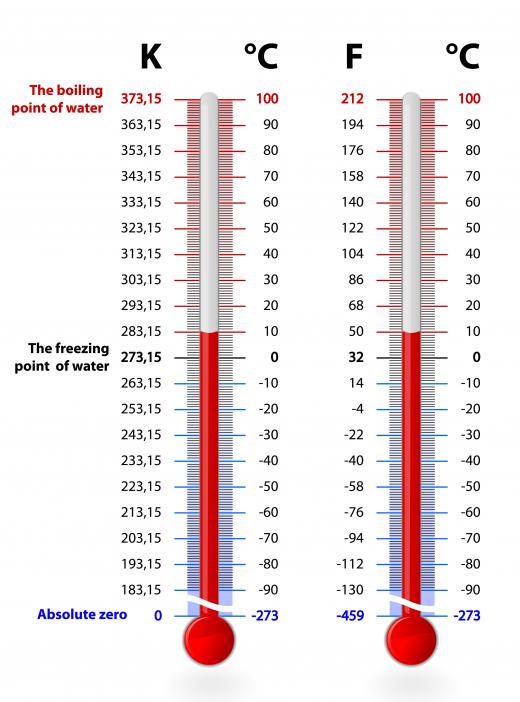
To determine the coefficient of performance, the absolute temperatures of the heating and cooling reservoirs must also be considered in some COP equations. This changes the equation so that the absolute temperature of the hot air reservoir and the absolute temperature of the cold air reservoir are considered. Taking these absolute temperatures into consideration and using the Kelvin scale, the answer that is computed will determine the maximum theoretical efficiency for units according to the first rule of thermodynamics. This equation is commonly used to determine the coefficient of performance for refrigerators and air conditioners.
The process of determining the COP is important because a comparison of coefficients of performance can be used to determine the amount of energy that could be saved by using one type of system versus another. For instance, if an electric heat pump is running at a COP of 4.5, this means that it provides 4.5 units of heat, and for each unit of heat, one unit of energy is consumed. If the user knows the price per kilowatt of energy used, then he can make an informed decision as to the type of system that may be better suited financially for his needs or as to which of two systems is a better buy. For example, if an electric heat pump will cost more because of the price of electricity versus the price of natural gas, then it would be in the user's best financial interest to select a system that runs on natural gas instead.









